Electron Transfer at the Electrode

With a Single Analyte Molecule

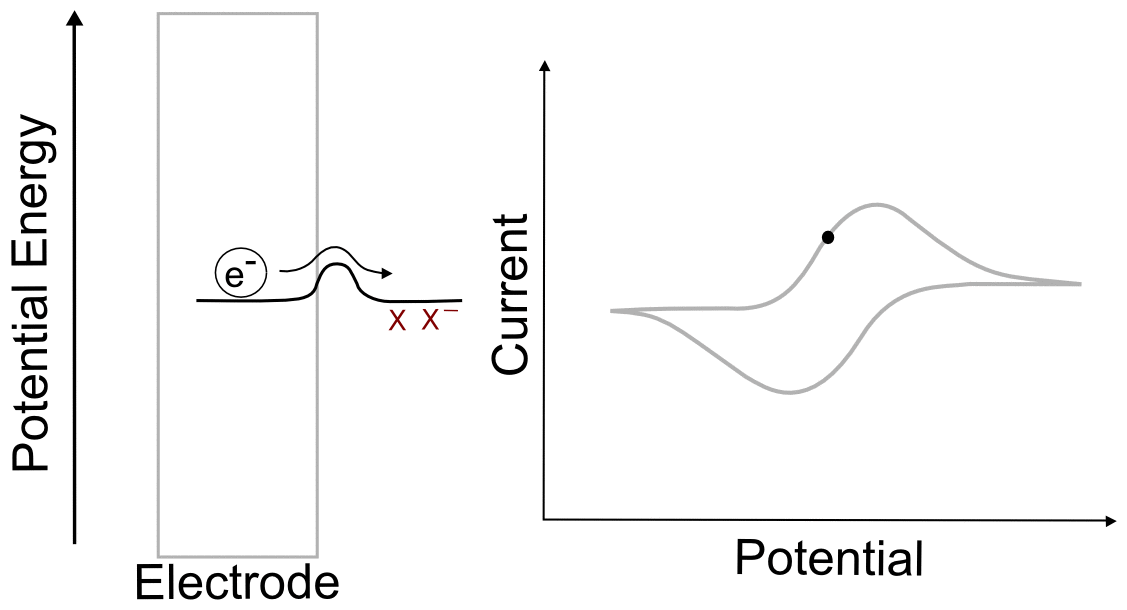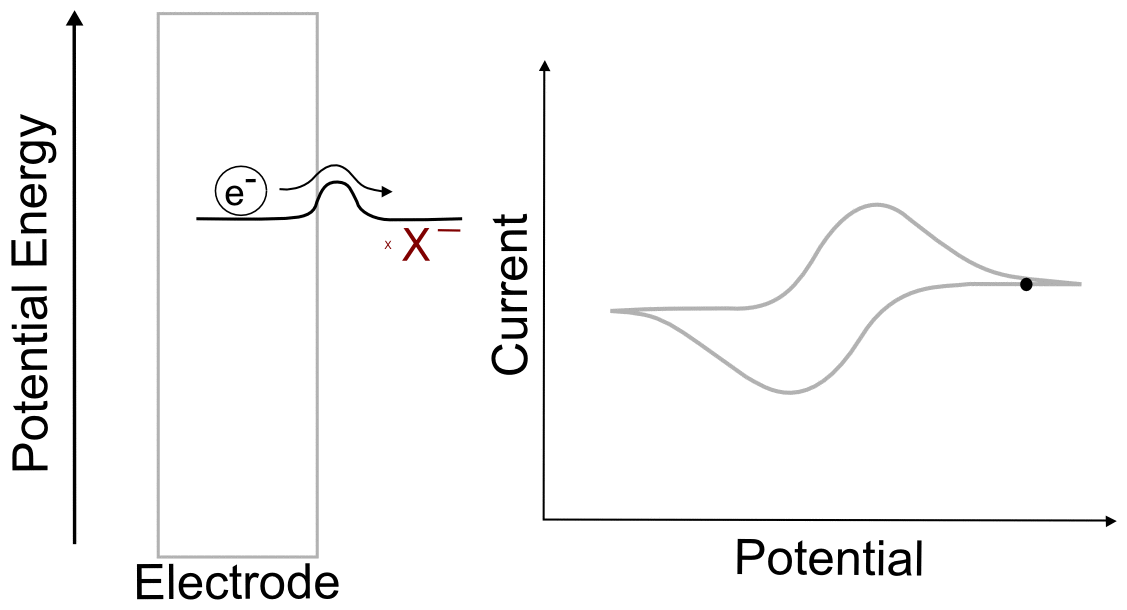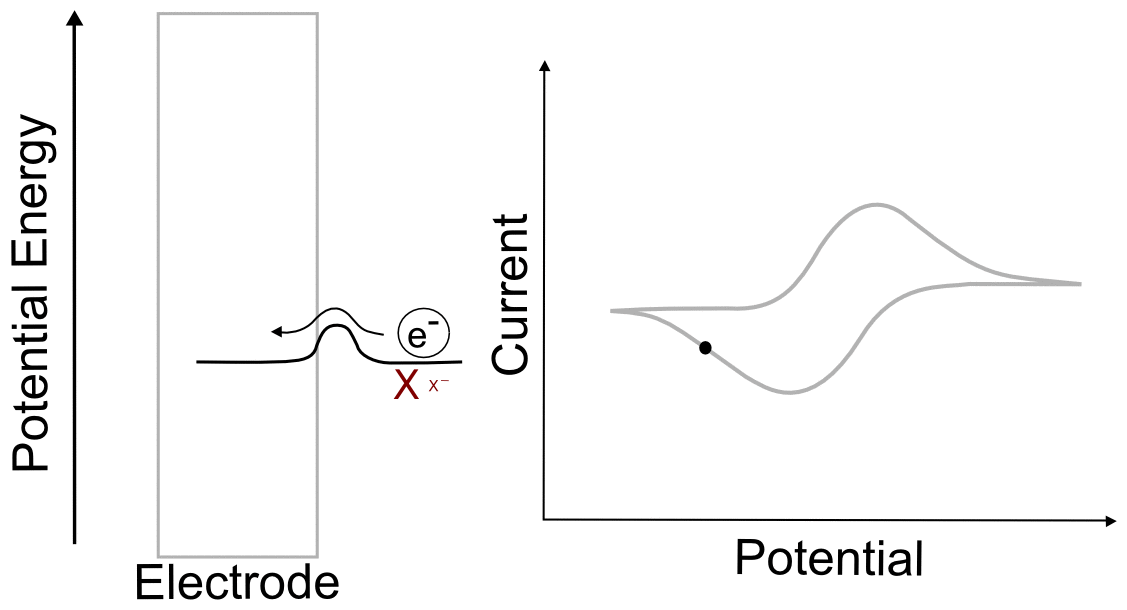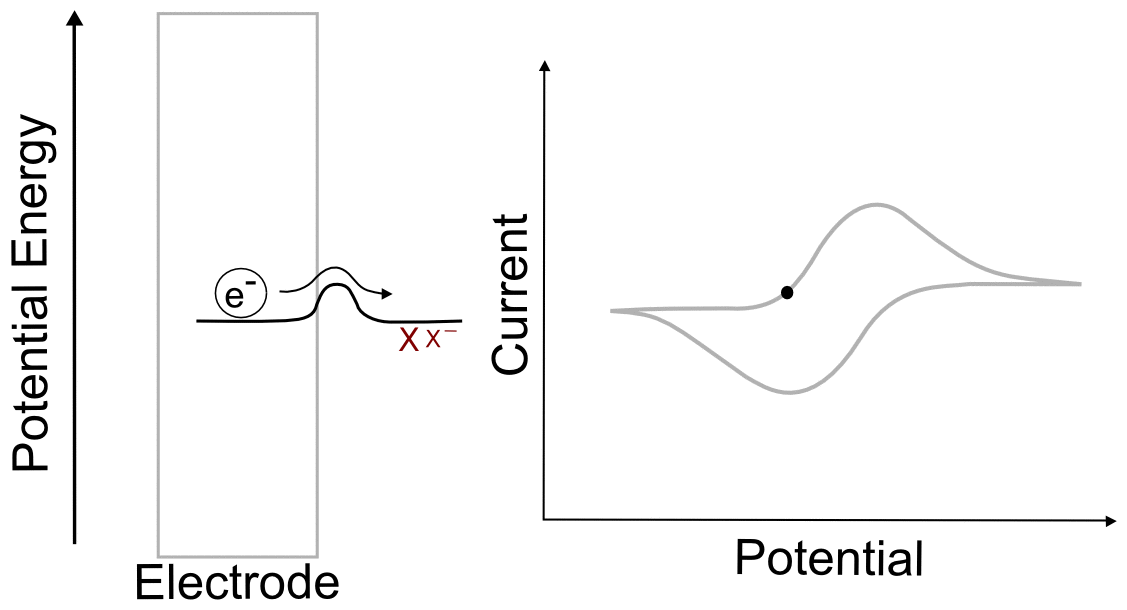
Suppose we have a single molecule next to the surface of an electrode. This redox-active molecule can accept an electron, and when it does so, it undergoes a change in potential energy. In order to evaluate the thermodynamics of this example, let's assume our thermodynamic "system" consists of the molecule and an electron in the electrode. In the "ball and hillscape" analogy, the potential energy of the reduced molecule (Xˉ) is represented by one valley at a specific altitude, while the height of the other valley denotes the sum of the potential energies of the molecule (X) and the electron in the electrode (eˉ). If the potential energy of the electrons in the electrode are very low (the electrode is at a positive potential/voltage), then it is more energetically favorable for our ball to reside in the valley where the electron remains in the electrode and our analyte molecule in the form of X. In other words, no electron transfer will occur, because doing so would be an endothermic process that would raise the energy of the entire system.

When the electrode potential (voltage) is too positive for a reduction to occur, its like the valley representing the analyte molecule and seperate electron in the electrode is at a lower energy and is therefore favored. It's energetically unfavorable for the reduction to occur because the valley represing the product of the electron transfer (Xˉ) is at a higher potential energy, so the ball would have to roll 'uphill.'

hover over pic for description

When we tell the potentiostat to give the electrode a more negative potential (voltage), it can be thought of as effectively raising the altitude of the "Xˉ + eˉ valley" on the energy hillscape. As the potential energy of the "X + eˉ valley" approaches, reaches, and surpasses the energy of the "Xˉ valley", it becomes energetically favorable for the electron to jump over to the molecule. This transfer to the lower energy state would lower the energy of the whole system, and is therefore exothermic and energetically favorable. When we now tell the potentiostat to give the electrode a more positive potential (voltage), lowering the altitude of the "X + eˉ valley" on the energy hillscape, it reaches a point where it becomes energetically favorable for the electron to jump back into the electrode. We have essentially just described a single molecule CV.

When the electrode potential (voltage) is negative enough for a reduction to occur, its like the valley representing the analyte molecule and separate electron in the electrode was raised to a higher energy and product of the electron transfer is therefore the favored species. It's energetically favorable for the reduction to occur because the valley representing the product of the electron transfer (Xˉ) is at a lower potential energy, so the ball would roll 'downhill.'

hover over pic for description

You might be wondering what the hill represents in this example. To explain this, we have to realize that electron transfers are extremely fast, almost instantaneous, and definitely faster than the movements of atoms in molecules. The stable form of any molecule X will be slightly different than its reduced form Xˉ. These changes can vary from differences in bond lengths between atoms to difference in number of bonds between the atoms. Electron transfers occur most easily when all of the atoms are in the correct place, meaning that for an electron to transfer, all of the distances between atoms in X must be very close to those in the stable form of Xˉ for an instant. If X and Xˉ are very similar structurally, hill between the respective valleys will be relatively small, but if there are large differences, the hill can be quite large. The consequence of high and low barriers to electron transfer are discussed below.

With Many Analyte Molecules

Combining the concepts explained above, we can construct a basic understanding of electron transfer during a cyclic voltammogram in a solution of analyte X. Just as in the previous single molecule example, we start with an electrode containing electrons of a low potential energy, but instead of a single molecular orbital next to it, we have the electrochemical potential of the all of the molecules of X and X^– next to the electrode. In this example, we start with a solution of pure X. In reality there is an infinitesimal amount of X^– that is generated by the electrode, but that's not relevant to this example. As the electrode potential increases (goes to more negative voltage) and approaches the electrochemical potential energy of the analyte, it becomes more favorable for electrons to transfer to X, reducing it to X^–. As more and more X becomes X^–, their ratios begin to change in the area near the electrode. This in turn changes the electrochemical potential energy (E) of the X/X^– mixture according to the Nernst equation. As the electrode potential becomes more negative and the concentration of X near the electrode drops to near zero, no more electron transfers can occur unless more molecules of X make their way to the electrode from the bulk solution. When we turn the scan around and start lowering the potential of the electrode (moving it to more positive potentials) the process reverses as it becomes more favorable for electrons to transfer from X^– to the electrode, the ratios of X to X^– change again, and the electrochemical potential energy of the analyte mixture returns to where it started. What we observe during a CV is the movement of these electrons back an forth, which registers as current.

Animation showing the transfer of electrons as the electrode potential (potential energy of the electrons in the electrode) is changed. The size of the X and Xˉ represent their relative concentrations at the electrode, which change as the electrode potential changes.

hover over pic for description

Kinetics and Electrochemical Reversibility

What we described above is the thermodynamics of electron transfer during a CV, as we just assumed that the electrons go wherever it is most energetically favorable for them to go, but in reality, this is not always how it happens. Sometimes, electrons will not transfer immediately even though it is energetically favorable for them to do so. A common reason for this is that electrons only jump to or from a molecule when the conditions are near perfect, if there is a large difference in bond lengths or physical orientation of X and X^–, electrons will not jump right away and will need to be given more potential energy (the electrode will need to go to more extreme voltages) in order to be forced to jump. In our energy hillscape analogy, we depict these obstacles as hill peaks separating the valleys. The higher the hill peak, the more an electron needs to be raised in energy in order to overcome it.

When there is a high barrier to electron transfer, the electrode has to travel to more extreme potentials before any electrons jump between the electrode and the analyte, causing what seems like a lag between electrode potential and current registering on the potentiostat, causing the two half waves of an irreversible electron transfer occur far away from each other on the potential (voltage) scale, though they are still centered around E_1/2. Using our energy hillscape analogy, the "X + eˉ valley" needs to be raised extra high or low to induce the ball to transfer over the peak separating the valleys.

Animation showing how irreversible waves in a CV are the result of a high energy barrier between a molecule X and its reduced form Xˉ. To overcome this barrier, the electrode needs to be at more extreme potentials in order to force electron transfer. The relative sizes of the red X and Xˉ represent their relative ratios at the electrode and the arrow denotes the net flow of electrons.

hover over pic for description

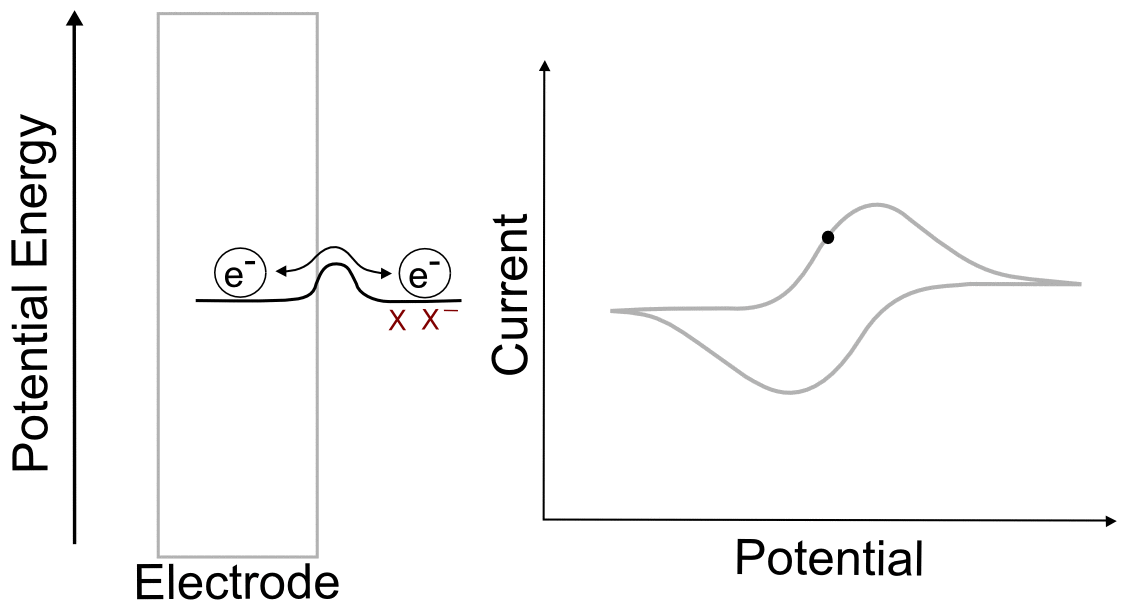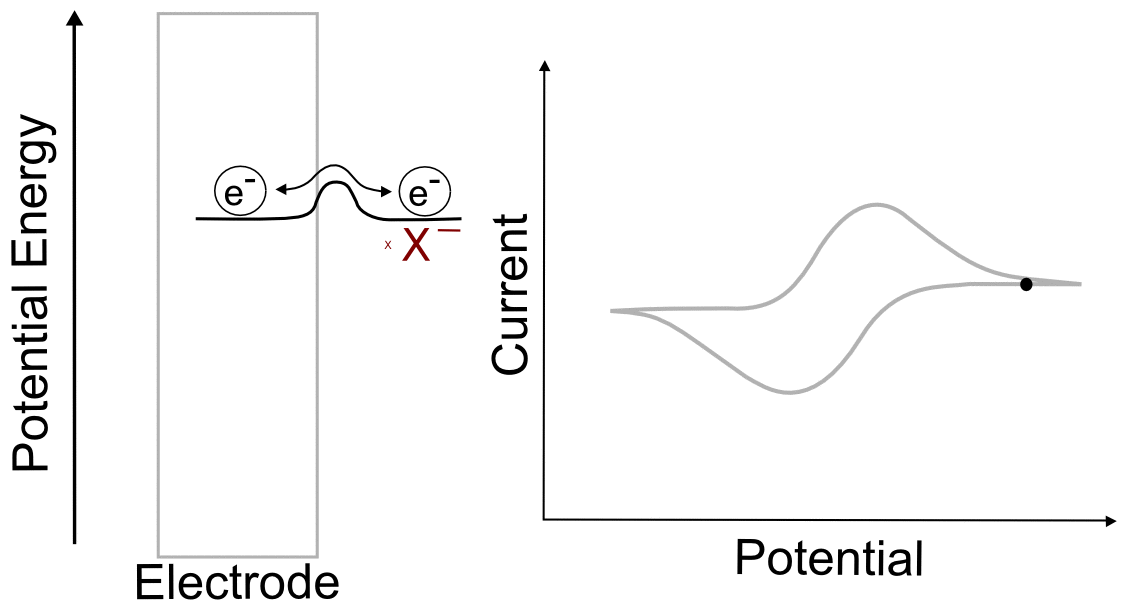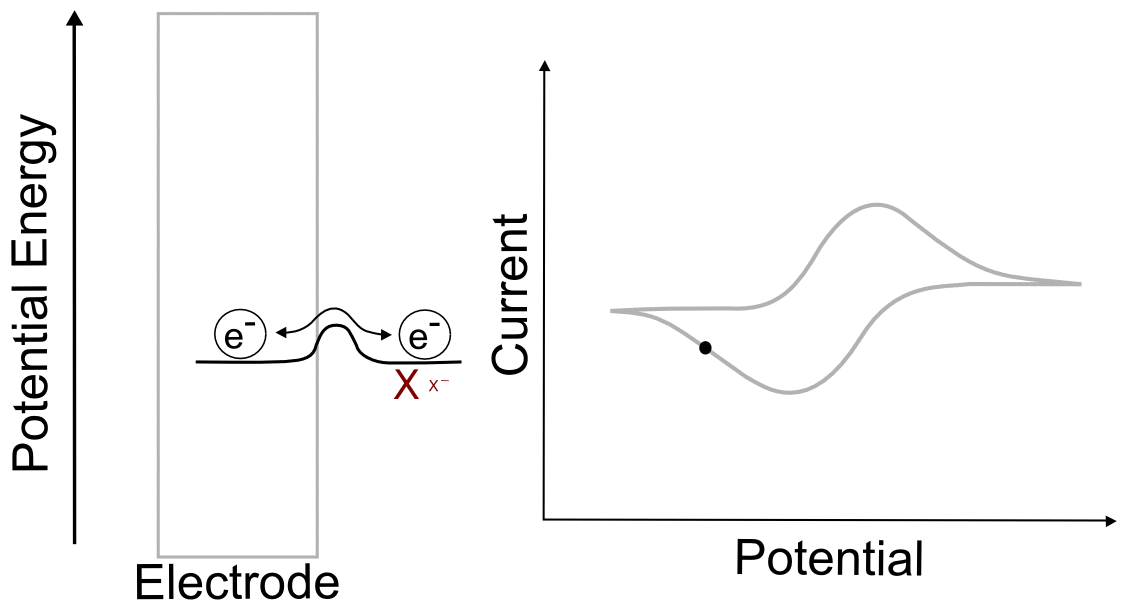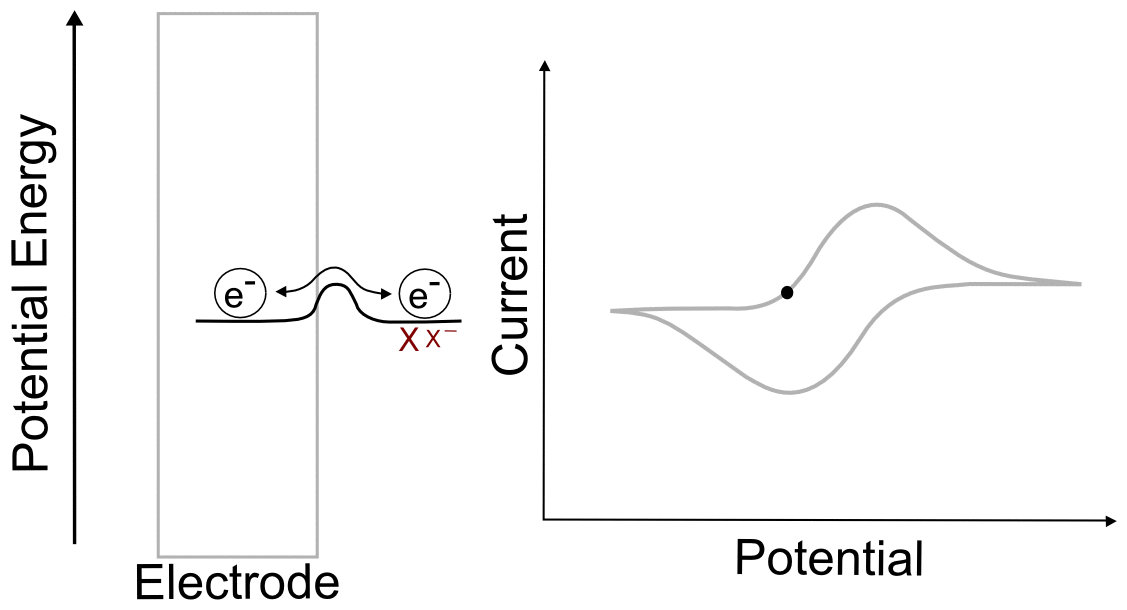
When we talk about reversible and irreversible electron transfers, we are talking about cases where there are differences in the ability of electrons to jump between the electrode and the analyte due to the size of the "peak" separating each "valley." When there is a low barrier, electrons transfer easily between the electrode and analyte molecules, giving rise to a reversible wave, where current is registered by the potentiostat right near the E_1/2 of the analyte. In this case, any change in the electrode potential (electrochemical potential energy of the electrons in the electrode) causes and immediate change in the concentrations of X and X^– near the electrode, so that the electrochemical potential of the electrons and the analyte equal each other at every point (near the E_1/2).

Animation showing how reversible waves in a CV are the result of a low energy barrier between a molecule X and its reduced form Xˉ. Not much energy is required to overcome the barrier and electron transfer happens as soon as the 'X + eˉ valley' gets close to the 'Xˉ valley.' The relative sizes of the red X and Xˉ represent their relative ratios at the electrode and the arrow denotes the net flow of electrons.

hover over pic for description

One of the consequences of having a low barrier to electron transfer is that electrons freely transfer back and forth. In the animation above, I tried to depict net flow of electrons using the arrow, but in reality, electrons are flying back and forth between the electrode and the analyte. The potential of the electrode dictates the concentration of X and X^– according to the Nernst equation, and the electrons instantly transfer to maintain equilibrium. A more accurate animation might be the following.

Animation showing that for the cases where the barrier is low, electrons are constantly transferring back and forth from the electrode to the molecules in solution, but they always maintain the concentrations of X and Xˉ mandated by the Nernst equation. The red X and Xˉ represent their relative concentrations at the electrode.

hover over pic for description

If you're confused as to why the shape of the wave doesn't seem to be explained by the change in the concentrations of X and X^– at the electrode, don't worry, because it isn't. Diffusion of molecules towards and away from the electrode is the reason for the wave shapes, and it will be covered in a later section, but first, a more thorough explanation of the uses of the Nernst equation.

Did I earn one of these yet?

Standard Operating Procedures for Cyclic Voltammetry by Daniel Graham
is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.